Programmazione iterativa

Programmazione iterativa

Il concetto di iterazione è alla base di qualsiasi operazione nei linguaggi di programmazione. In R molte delle operazioni sono vettorizzate. Questo rende il linguaggio più efficiente e pulito MA nasconde il concetto di iterazione.

Ad esempio la funzione sum() permette di sommare un vettore di numeri.

# somma i numeri da 1 a 10
sum(1:10)
[1] 55

Ma cosa si nasconde sotto?

Esempio: se io vi chiedo di usare la funzione print() per scrivere “hello world” nella console 5 volte, come fate?

msg = "hello world"
print(msg)
[1] "hello world"
print(msg)
[1] "hello world"
print(msg)
[1] "hello world"
print(msg)
[1] "hello world"
print(msg)
[1] "hello world"

Quello che ci manca (e che invece fa la funzione sum()) è un modo di ripetere una certa operazione, senza effettivamente ripetere il codice manualmente.

Ci sono vari costrutti che ci permettono di ripetere operazioni, i più utilizzati sono:

  • Ciclo for

  • Ciclo while

  • Ciclo repeat

  • *apply family

Il ciclo for

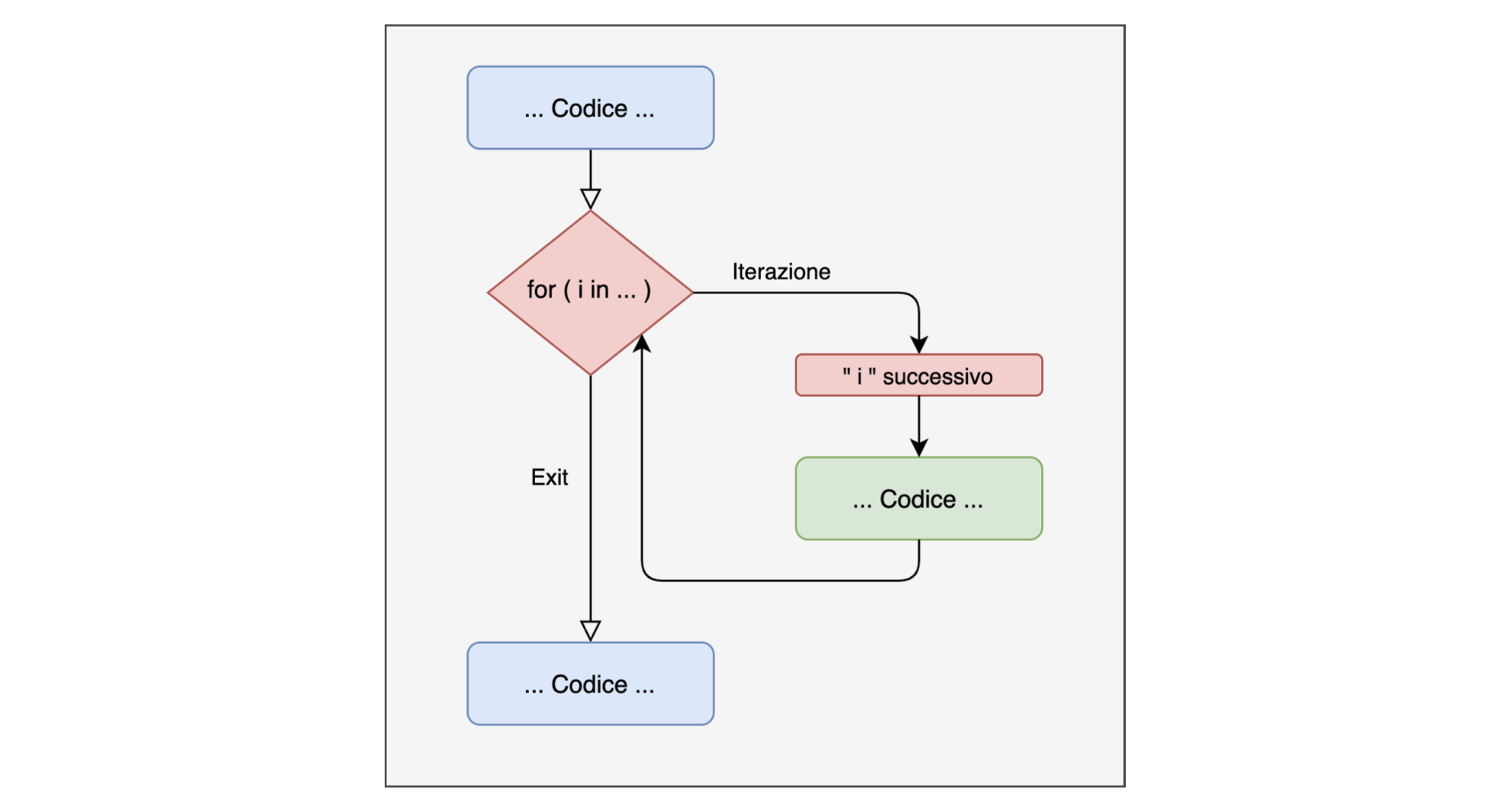
Il ciclo for è una struttura che permette di ripetere un numero finito e pre-determinato di volte una certa porzione di codice.

La scrittura di un ciclo for è:

n = 10
for(i in 1:n){
# quali operazioni
}

Se voglio stampare una cosa 5 volte, posso tranquillamente usare un ciclo for:

for(i in 1:5){
print(paste("hello word", i, sep = "_"))
}
[1] "hello word_1"
[1] "hello word_2"
[1] "hello word_3"
[1] "hello word_4"
[1] "hello word_5"

Scomponiamo il ciclo for

  • for(){ }: è l’implementazione in R (in modo simile all’if statement)

  • i: questo viene chiamato iteratore o indice. E’ un indice generico che può assumere qualsiasi valore e nome. Per convenzione viene chiamato i, j etc. Questo tiene conto del numero di iterazioni che il nostro ciclo deve fare

  • in <valori>: questo indica i valori che assumerà l’iteratore all’interno del ciclo

  • { # operazioni }: sono le operazioni che i ciclo deve eseguire

La potenza del ciclo for sta nel fatto che l’iteratore i assume i valori del vettore specificato dopo in, uno alla volta:

for(i in 1:10){ 
  print(i)
}
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10

For con iteratore vs senza

i rappresenta l’indice degli elementi del vettore vec

vec=1:5

for(i in 1:length(vec)){ 
  
  print(vec[i])

  }
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5

i rappresenta direttamente ogni elemento del vettore vec

vec=1:5

for(i in vec){ 
  
  print(i)

}
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5

Ciclo while

Il ciclo while utilizza una condizione logica e non un iteratore e un range di valori come nel for. Il ciclo continuerà fino a che la condizione è TRUE:

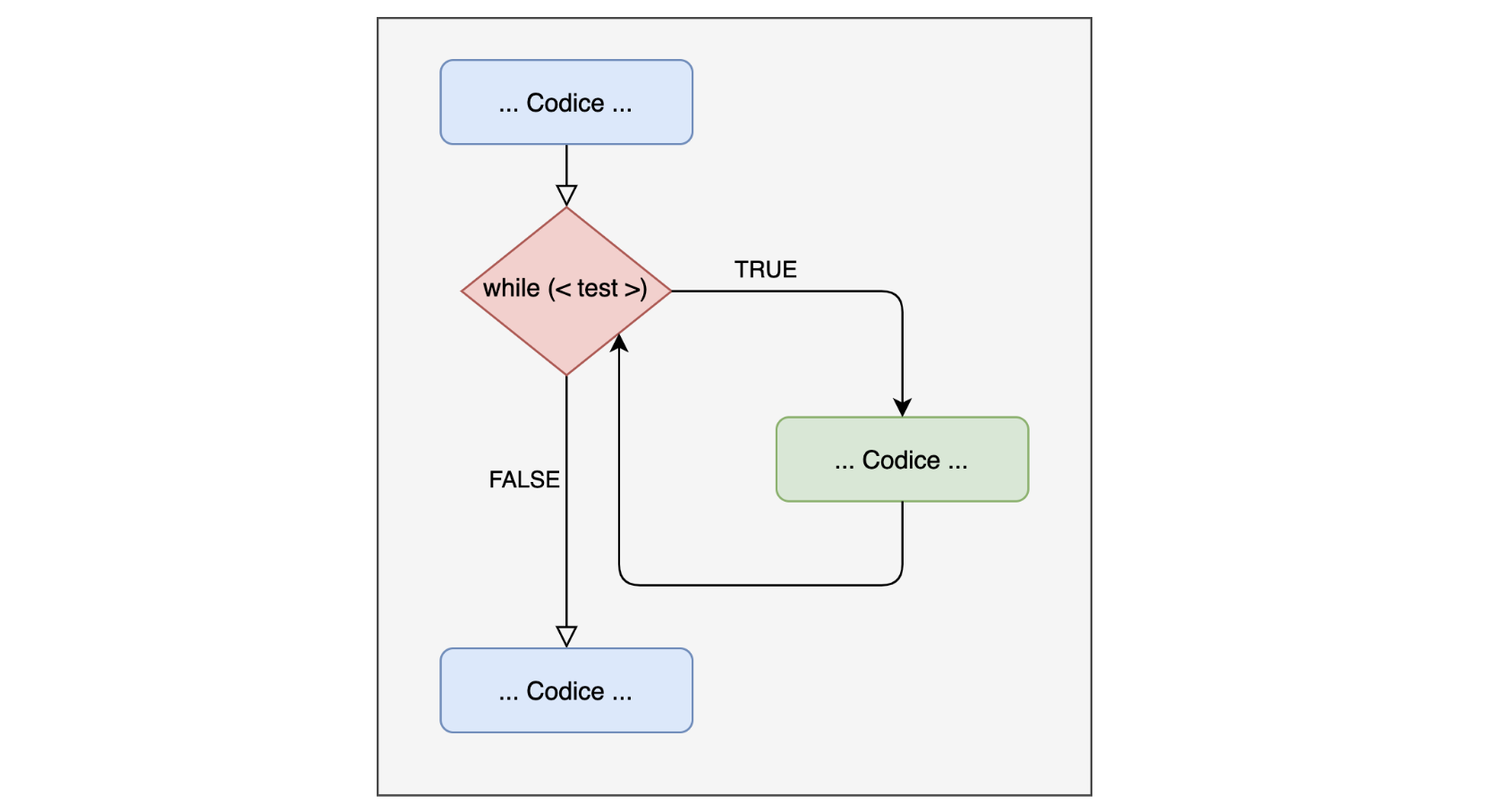
Provate a scrivere questo ciclo while e vedere cosa succede e capire perchè accade

x = 10

while (x < 15) { 

  print(x)

}

Il ciclo while è un ciclo non pre-determinato e quindi necessita sempre di un modo per essere interrotto, facendo diventare la condizione falsa.

x = 5

while (x < 15) { 
  print(x)
  x = x + 1 
}
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10
[1] 11
[1] 12
[1] 13
[1] 14

Ciclo repeat

La logica del ciclo repeat è molto simile a quella del ciclo while, ma con 3 importanti differenze:

  1. esegue sempre almeno un’interazione

  2. enfatizza la ripetizione fino a che una condizione non viene raggiunta

  3. utilizza il comando break per terminare

Ciclo repeat

Lancia il dado finchè non viene fuori 6:

repeat{
  lancia_dado = sample(1:6, 1)
  print(lancia_dado)
  if(lancia_dado == 6) break
}
[1] 2
[1] 3
[1] 3
[1] 6

repeat vs. while

repeat valuta la condizione una volta finita l’iterazione, mentre while all’inizio. Se la condizione non è TRUE all’inizio, il while non parte mentre repeat si:

i=1
repeat { 
  print(i)
  i=i+1 
  if(i > 3)break
  }
[1] 1
[1] 2
[1] 3
i=1
while (i < 4) { 
  print(i)
  i=i+1 
  }
[1] 1
[1] 2
[1] 3

Esempio funzione sum()

Immaginiamo di non avere la funzione sum() e di volerla ricreare, come facciamo? Idee?

Somma come iterazione

Scomponiamo concettualmente la somma, sommiamo i numeri da 1 a 10:

  • prendo il primo e lo sommo al secondo (somma = 1 + 2)

  • prendo la somma e la sommo al 3 elemento somma = somma + 3 …

In pratica abbiamo:

  • il nostro vettore da sommare

  • un oggetto somma che accumula progressivamente le somme precedenti

Somma come iterazione

somma = 0 # inizializziamo la somma a 0
x = 1:10 #vettore x 

for(i in 1:length(x)){ # per tutta la lunghezza di x = 1:10 
  somma = somma + x[i]
}

Mettiamo tutto dentro una funzione (i.e., creo una funzione che replichi quello che fa la funzione somma)

my_sum = function(x){
  somma = 0 # inizializziamo la somma a 0
  for(i in seq_along(x)){  # equivalente a 1:length(x)
    somma = somma + x[i]
  }
  return(somma)
}

x = rnorm(100, mean = 0, sd = 1)

my_sum(x)
[1] 0.6178465
sum(x)
[1] 0.6178465

Iterazione, applicazioni

Il ciclo for è anche utile per simulare dei dati per esempio. Supponiamo di avere una variabile y (reddito) che dipenda dall’età:

  1. Carico il dataset che ho creato:
mydf = read.csv(file = "data/mydf_2.csv") #carico il dataset 

str(mydf)
'data.frame':   30 obs. of  4 variables:
 $ id     : int  1 2 3 4 5 6 7 8 9 10 ...
 $ age    : int  14 30 26 33 45 20 47 17 21 31 ...
 $ age_cat: chr  "adolescente" "giovane" "giovane" "adulto" ...
 $ age_z  : num  -1.625 -0.164 -0.53 0.11 1.205 ...
  1. Simulo, attraverso un ciclo for , la variabile y (reddito) assumendo che dipenda da age_z (età):
set.seed(111) # per riproducibilità

niter = 1000
res_all = rep(NA, niter)    # tutti gli effetti stimati
p_val = rep(NA, niter)      # tutti i p-value

# Dati osservati
age_z = mydf$age_z
eff_eta = .2 #effetto età
n_obs = length(age_z)

for(i in 1:niter) {
  y = 0 + eff_eta * age_z + rnorm(n_obs, 0, 1) # aggiungo sempre un pò di rumore
  
  # modello lineare
  mod = lm(y ~ 1 + age_z) 
  
  # estraggo stima effetto
  res_all[i] = coef(mod)[2] 
  
  # p-value di age_z
  p_val[i] = summary(mod)$coefficients[2, 4]
}

Risultato:

# Filtra solo risultati significativi
res_sig = res_all[p_val <= 0.05]

# Statistiche descrittive
cat("Proporzione significativi = Power:", mean(p_val <= 0.05), "\n")
Proporzione significativi = Power: 0.154 
cat("Media tutti gli effetti:", mean(res_all), "\n")
Media tutti gli effetti: 0.1875023 
cat("Media effetti significativi:", mean(res_sig), "\n")
Media effetti significativi: 0.4612498

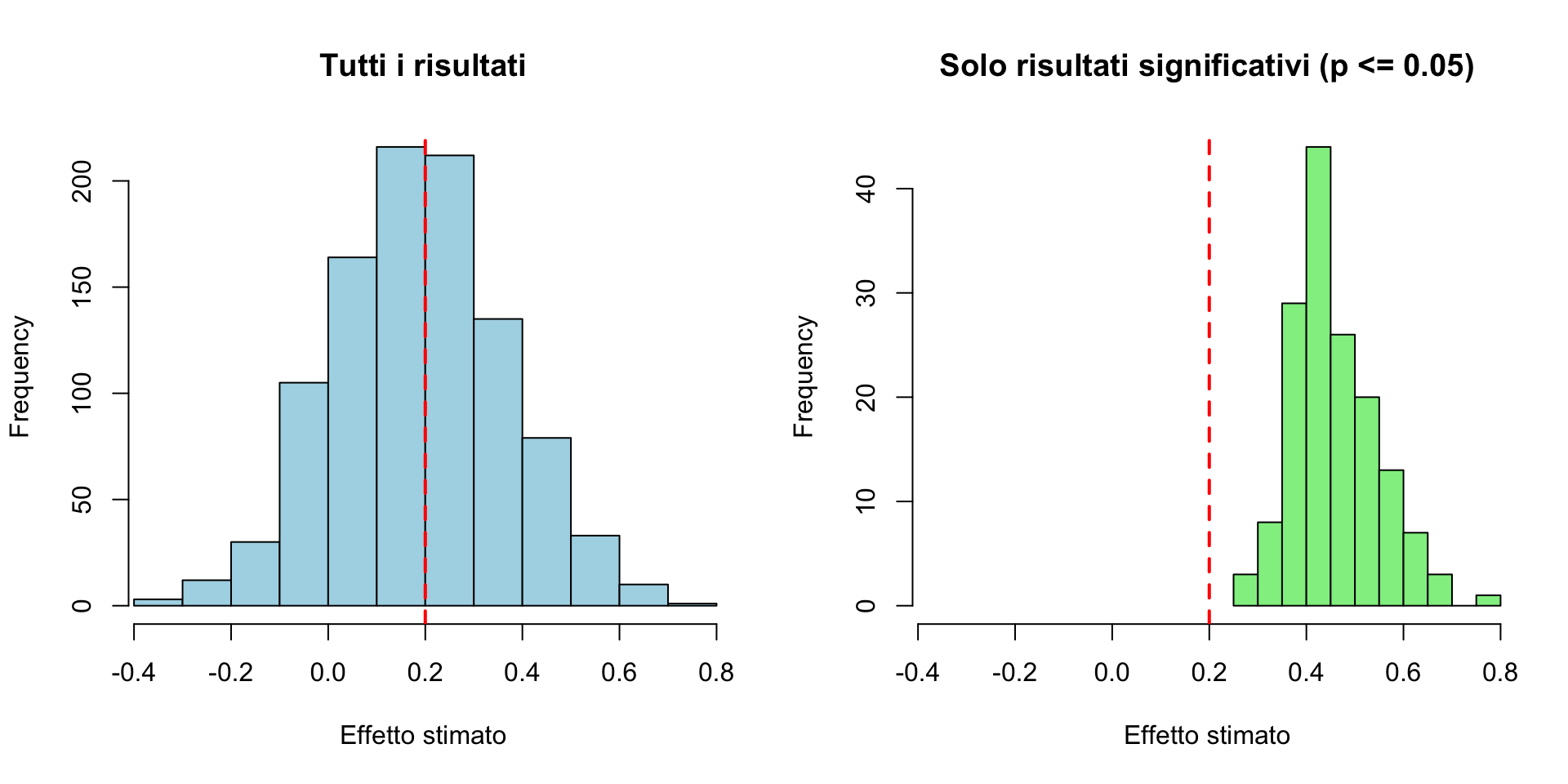
Proprio grazie al for loop è possibile effetuare una power simulation.

Per saperne di più date un’occhiata a questa pagina! :)

Ciclo for nested

Una volta compresa la struttura iterativa, si può espandere facilmente inserendo un ciclo dentro un altro:

for(i in 1:3){ # livello 1
  for(j in 1:3){ # livello 2
      print(paste(i, j))
  }
}
[1] "1 1"
[1] "1 2"
[1] "1 3"
[1] "2 1"
[1] "2 2"
[1] "2 3"
[1] "3 1"
[1] "3 2"
[1] "3 3"

Immaginiamo di avere due gruppi sperimentali (ad esempio, Gruppo di controllo e Gruppo trattamento), ciascuno con 10 partecipanti. Vogliamo misurare una variabile (ad esempio, il tempo di reazione) per ogni partecipante e registrare i risultati in un dataframe:

# Definire parametri della ricerca
gruppi = c("Controllo", "Trattamento") # Nomi dei gruppi
num_soggetti=10                      # Numero di soggetti per gruppo
tot_soggetti = num_soggetti * length(gruppi)

# Creare un data.frame per memorizzare i dati
res=data.frame(
  
  # Fattore gruppo
  Gruppo = factor(x = rep(gruppi, each = num_soggetti)),
  
  # fattore soggetto 
  Soggetto = factor(x = 1:tot_soggetti),
  
  # Tempo di reazione vettore numerico con rt = 0 
  RT = numeric(tot_soggetti)
)
head(res, 5) # guardo le prime osservazioni di res
     Gruppo Soggetto RT
1 Controllo        1  0
2 Controllo        2  0
3 Controllo        3  0
4 Controllo        4  0
5 Controllo        5  0
tail(res, 5) # guardo le ultime osservazioni di res
        Gruppo Soggetto RT
16 Trattamento       16  0
17 Trattamento       17  0
18 Trattamento       18  0
19 Trattamento       19  0
20 Trattamento       20  0
# Ciclo nested per simulare raccolta dati
set.seed(42)  # Per riproducibilità dei dati simulati

k = 1 #iteratore tempi di reazione

# quanti livelli ha Gruppo?
for (i in 1:length(levels(res$Gruppo))) {
  
  # inizio con il primo gruppo che è il gruppo di controllo
  gruppo = levels(res$Gruppo)[i] 
  
  for (j in 1:num_soggetti) { # num_soggetti each gruppo
    
    # è il gruppo di controllo?
    RT = ifelse(gruppo == "Controllo", 
               yes = rlnorm(1, mean = log(.500), sd = .050), 
               no = rlnorm(1, mean = log(.450), sd = .050))
    
    res$RT[k] = RT
    k = k + 1 
  }
}
str(res)
'data.frame':   20 obs. of  3 variables:
 $ Gruppo  : Factor w/ 2 levels "Controllo","Trattamento": 1 1 1 1 1 1 1 1 1 1 ...
 $ Soggetto: Factor w/ 20 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
 $ RT      : num  0.535 0.486 0.509 0.516 0.51 ...
head(res, 3)
     Gruppo Soggetto        RT
1 Controllo        1 0.5354760
2 Controllo        2 0.4860800
3 Controllo        3 0.5091611
tail(res, 3)
        Gruppo Soggetto        RT
18 Trattamento       18 0.3940291
19 Trattamento       19 0.3983075
20 Trattamento       20 0.4807047
mean(res$RT[res$Gruppo == "Controllo"])
[1] 0.5142776
mean(res$RT[res$Gruppo == "Trattamento"])
[1] 0.4476666

Ora facciamo un po’ di pratica!


Aprite e tenete aperto questo link:

https://etherpad.wikimedia.org/p/arca-corsoR